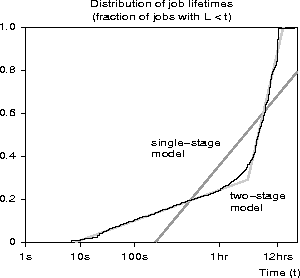
Figure 6: The distribution of jobs submitted to the long queue on the Intel Paragon at SDSC. The single-stage model is the same as in Figure 3. The two-stage model was chosen by hand to fit the observed data.
In Section 3.1 we observed that the uniform-log distribution model does not fit the distribution of jobs from the long queue well. In this section we develop an alternate model that fits this distribution well, and evaluate its effect on the accuracy of our predictors.
The uniform-log model can be extended to a multistage model that fits any piecewise linear distribution. For example, the observed distribution appears to contain two classes of job: short (between 10 seconds and 3 hours) and long (between 3 and 15 hours). Thus, we divided the distribution into two stages and estimated parameters for each (by eye). Figure 6 shows the observed distribution and the improved model. Clearly the two-stage model is a better fit.

Figure 6: The distribution of jobs submitted to the long queue on the Intel
Paragon at SDSC. The single-stage model is the same as in
Figure 3. The two-stage model was chosen by
hand to fit the observed data.
Calculating the CLM for the multi-stage model is only slightly more
complicated than for the single-stage model. Given the age of a job,
we use Bayes' theorem to calculate ![]() , the probability that the job
belongs to each class. Then the conditional distribution is
, the probability that the job
belongs to each class. Then the conditional distribution is
where i enumerates the stages of the model. For a given stage, we calculate the conditional distribution using Equation 3 with the parameters for that stage.
Using the improved model does not significantly improve the performance of either predictor. Thus we conclude that an ill-fitting model does not impair the predictors per se, but rather that the bimodal shape of the distribution is the root of the problem. A bimodal distribution indicates that there are two classes of jobs and that users are failing to distinguish between them. The multistage model, even if it fits the distribution well, does not recover this lost information, and therefore does not improve our predictions. The only way to improve the predictions is to solicit better information from users.