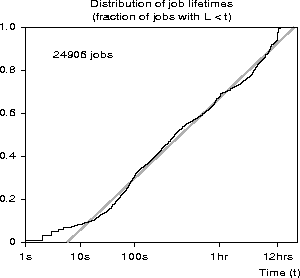
Figure 1: The distribution of lifetimes for 24906 batch jobs submitted to the Intel Paragon at SDSC. The gray line shows the least-squares fit for the observed data (intercept
During 1995, 24906 jobs were submitted to the batch partition of the 400-node Intel Paragon at SDSC. Figure 1 shows the distribution of lifetimes for these jobs.
Except for the longest and shortest jobs, this distribution is nearly straight (on a logarithmic x-axis); in other words, the logs of the lifetimes are distributed uniformly. Although we do not know any theoretical reason why lifetimes should have this uniform-log distribution, we will take advantage of this observation by fitting a straight-line approximation to the observed distribution. Using this approximation (instead of the observed values) simplifies the calculation of the conditional distribution of lifetimes (Equation 3).

Figure 1: The distribution of lifetimes for 24906 batch jobs submitted to the Intel
Paragon at SDSC. The gray line shows the least-squares fit for
the observed data (intercept ![]() = -0.18, slope
= -0.18, slope ![]() = 0.10).
= 0.10).
We calculated a straight-line approximation by least-squares
regression (omitting the longest 10% and the shortest 10% of jobs).
The ![]() value of the fit is over 0.99, indicating that the linear
approximation is very good. Thus our model of this distribution of
lifetimes is
value of the fit is over 0.99, indicating that the linear
approximation is very good. Thus our model of this distribution of
lifetimes is
![]()
where ![]() is the cumulative distibution function of L,
a random variable representing the lifetime of a job, and
is the cumulative distibution function of L,
a random variable representing the lifetime of a job, and ![]() and
and
![]() are the parameters of the model (intercept and slope).
Also, t is bounded by
are the parameters of the model (intercept and slope).
Also, t is bounded by ![]() and
and
![]() . For the estimated
parameters from Figure 1,
. For the estimated
parameters from Figure 1, ![]() seconds
and
seconds
and ![]() hours.
hours.
For this model we can calculate the distribution of lifetimes conditioned on the current age of a job:
To find the median lifetime of a job given its current age, we set the conditional cdf to 0.5 and solve for t:
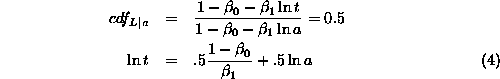
Substituting ![]() , we
express the median lifetime as
, we
express the median lifetime as ![]() .
Thus, this distribution does not obey the past-repeats heuristic; rather,
the median remaining lifetime increases slowly with age,
until
.
Thus, this distribution does not obey the past-repeats heuristic; rather,
the median remaining lifetime increases slowly with age,
until ![]() , after which the median
remaining lifetime drops quickly.
, after which the median
remaining lifetime drops quickly.
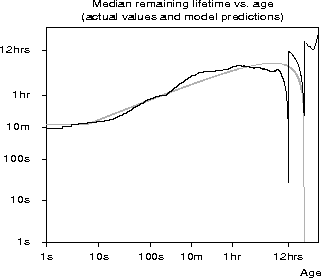
Figure 2: The median remaining lifetime of a job as a
function of its current age. The gray line shows the values
predicted by our model.
Figure 2 shows the median remaining lifetime as calculated
according to the model and according to the observed data. The
proposed model fits the data well for ages less than 6 - 12 hours.
For longer lifetimes, the distribution of lifetimes diverges from the
model. The remaining lifetimes of old jobs do not decline, as
predicted, but appear to increase. It is difficult to generalize this
behavior, because there are few jobs with lifetimes greater
than 12 hours![]() and their distribution does not fit our
model.
and their distribution does not fit our
model.
The average remaining lifetime of a job, ![]() , behaves similarly; it increases
slowly with age and then drops sharply as the age approaches the
limit. Since our model is not accurate for jobs with lifetimes
greater than 12 hours, and since the distribution of these jobs
is difficult to characterize, we will need to be careful about how we
apply our model to old jobs.
, behaves similarly; it increases
slowly with age and then drops sharply as the age approaches the
limit. Since our model is not accurate for jobs with lifetimes
greater than 12 hours, and since the distribution of these jobs
is difficult to characterize, we will need to be careful about how we
apply our model to old jobs.