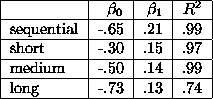
Figure 3: The distribution of lifetimes for parallel batch jobs submitted to the Intel Paragon at SDSC, broken down by queue. The gray lines show the least-squares fit for each queue.
If jobs can be divided into classes on the basis of a priori information, and the distribution of lifetimes differs between classes, then it is possible to improve the accuracy of the predictions by estimating and using different workload parameters for each class.
Depending on the environment, jobs might be partitioned according to executable name, user name, or declared resource requirements. Many queueing systems ask users to provide estimates of the resource requirements of their jobs: e.g., number of processors, memory requirements, and estimated run times.
On the Intel Paragon at SDSC, users declare the resource requirements of their jobs implicitly by their selection of one of the NQS queues. Most jobs are submitted to queues that specify the maximum cluster size of the job (powers of two) and the length of time it will run (short, medium, or long).

Figure 3: The distribution of lifetimes for parallel batch jobs submitted to
the Intel Paragon at SDSC, broken down by queue. The gray lines show
the least-squares fit for each queue.
Not surprisingly, we found that the distributions for the short, medium and long queues are significantly different (Figure 3). The differences among these distributions indicate that users have some information about the expected run times of their jobs; on the other hand, this information is far from perfect. There is considerable overlap between the different queues -- many jobs are submitted to what turns out to be the wrong queue. For example, 30% of the jobs from the short queue run longer than the median of the medium queue, and 17% of the jobs from the medium queue are shorter than the median of the short queue.
Thus it is not obvious how to use queue information to predict the remaining lifetime of a job. The technique we are proposing, using a different conditional distribution for each queue, seems like an effective way to use information provided by the user without suffering greatly if that information turns out to be wrong.
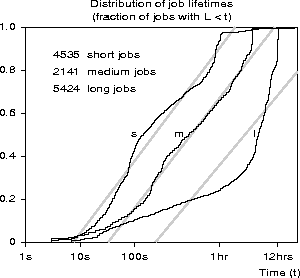
Using the same technique as in the previous section (discarding the longest and shortest 10% of each group), we fit a line to the lifetime distribution for each queue. Table 1 shows the resulting coefficients. We treat sequential jobs as a distinct class because their distribution of lifetimes is significantly different from that of the parallel jobs.
For all but the long queue, the goodness of fit metric is quite good;
for the long queue, it is only 0.74, which is not surprising, since
the distribution is obviously not a straight line. The distribution
for long jobs is bimodal: roughly ![]() run between 10 seconds and
3.5 hours; the remaining 60% run between 3.5 and 12 hours. In
Section 5.4 we extend our model to address this poor
fit, but in the meantime we will use the estimated parameters as is.
run between 10 seconds and
3.5 hours; the remaining 60% run between 3.5 and 12 hours. In
Section 5.4 we extend our model to address this poor
fit, but in the meantime we will use the estimated parameters as is.
Table 1