Introductory Programming
Fall 2004

Homework 2

The reading for this assignment is Chapters 1 and 2 of How to think.... For this assignment you will have to translate expressions from mathematical notation into Python, and use variables to express complex computations in simple, readable form.

AmoebaWorld

  1. Download the AmoebaWorld code from the class web page using a web browser or wget: 

    wget http://wb/ip/code/World.py
wget http://wb/ip/code/AmoebaWorld.py

  2. Run the program by typing python AmoebaWorld.py

  3. Press the Run button. An amoeba should appear at the origin and the move along the line $x = y$ for 10 seconds. The path of the amoeba is determined by the parametric equations in the text fields in the lower right. Initially, these equations are
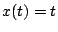
    $\displaystyle x(t) = t$     (1)
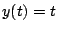
    $\displaystyle y(t) = t$      

    Notice that as the program runs, it prints the values of $t$, $x$, and $y$ in the window where you ran the program.

  4. In the text field for $y(t)$, type the expression sin(t) (notice that I am using italics for mathematical notation and a `typewriter' font for Python code). Run the program again. The amoeba should trace out a sine curve.

  5. Translate each of the following pairs of parametric equations into Python code, type them into the text fields, and run the program.
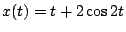
    $\displaystyle x(t) = t + 2 \cos 2t$     (2)
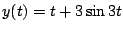
    $\displaystyle y(t) = t + 3 \sin 3t$      


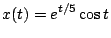
    $\displaystyle x(t) = e^{t/5} \cos t$     (3)
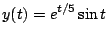
    $\displaystyle y(t) = e^{t/5} \sin t$      


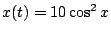
    $\displaystyle x(t) = 10 \cos^2 x$     (4)
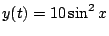
    $\displaystyle y(t) = 10 \sin^2 x$      


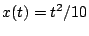
    $\displaystyle x(t) = t^2 / 10$     (5)
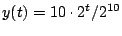
    $\displaystyle y(t) = 10 \cdot 2^t / 2^{10}$      

  6. At some point, it becomes inconvenient to type Python code in text fields. We would rather write the code and store it in a file. For an example of how to do this, download 

    wget http://wb/ip/code/MyAmoeba.py
    Run the program by typing python MyAmoeba.py. The amoeba should traverse a figure eight. If you get bored, you can interrupt the program by moving the mouse to the window where you started the program and pressing Control-C.

    Use emacs or some other text editor to edit this file. You might not understand all of it, but there are comments that explain what it does. You can change the behavior of the amoeba by changing the lines that compute $x(t)$ and $y(t)$. Change the program so that it computes one of the examples from the previous section, then save the file and restart the program.

    Remember to save the file and restart the program each time you make a change.

  7. By now you may have made some unintentional mistakes, but now it is time to make some intentional ones.

    1. In the line 9 * sin(t) * cos(t), delete one of the multiplication operators. Save the file and run the program again. What error message do you get?

    2. Delete one or both of the parentheses in sin(t). What happens?

    3. Replace the parentheses with square brackets ([]).

    4. Change the indentation of one of the lines so that it doesn't line up any more. What's the error message?

    5. Refer to a variable that doesn't exist, or misspell the name of one that does.

    6. If there's anything else you can think of that you might do by accident, do it on purpose now.

  8. If a circle of radius $b$ rolls around the outside of a circle with radius $a$, a point on the outer circle traces a curve called an epicycloid[*]. For formally, an epicycloid is defined by the following parameteric equations:


    $\displaystyle x = (a + b) \cos t - b \cos [(a/b + 1) t]$     (6)
    $\displaystyle y = (a + b) \sin t - b \sin [(a/b + 1) t]$      

    Modify MyAmoeba.py so that the Amoeba traces an epicycloid. You should define variables named a and b; try out different values and see what you get.

    There are a couple of subexpressions in the formulas that appear more than once, like $a+b$ and $(a/b + 1)t$. You might want to assign these values to temporary variables so that the program only has to evaluate them once.

  9. Check out the other curves in the `Famous Curves Index' at 

    http://www-gap.dcs.st-and.ac.uk/~history/Curves/Curves.html

    Look them over and see if there is one you want to implement. In some cases the web page provides parametric equations, but in other cases you might have to convert from one of the other formats. Once you have chosen your favorite curve, modify MyAmoeba to draw it. You might have to adjust the parameters so that the curve looks good and uses a reasonable amount of the `slide'.

  10. Add a comment to the program to explain which curve it is drawing and any other information you think is important.

  11. Put a comment with your name in it at the beginning of the program. Print a copy of the program by following the instructions in Chapter 3 of the Olinux manual.


... epicycloid[*]
For more information, see http://www-gap.dcs.st-and.ac.uk/~history/Curves/Epicycloid.html