Browsed by
Category: Uncategorized

Young Christians are less religious than the previous generation

Young Christians are less religious than the previous generation

This is the first in a series of articles where I use data from the General Social Survey (GSS) to explore

  • Differences in beliefs and attitudes between Christians and people with no religious affiliation (“Nones”),
  • Generational differences between younger and older Christians, and
  • Generational differences between younger and older Nones.

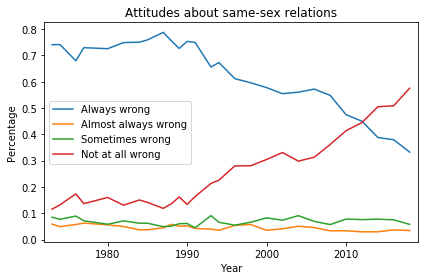
On several dimensions of religious belief, young Christians are less religious than their parents’ generation. I’ll explain the methodology below, but here are the results:

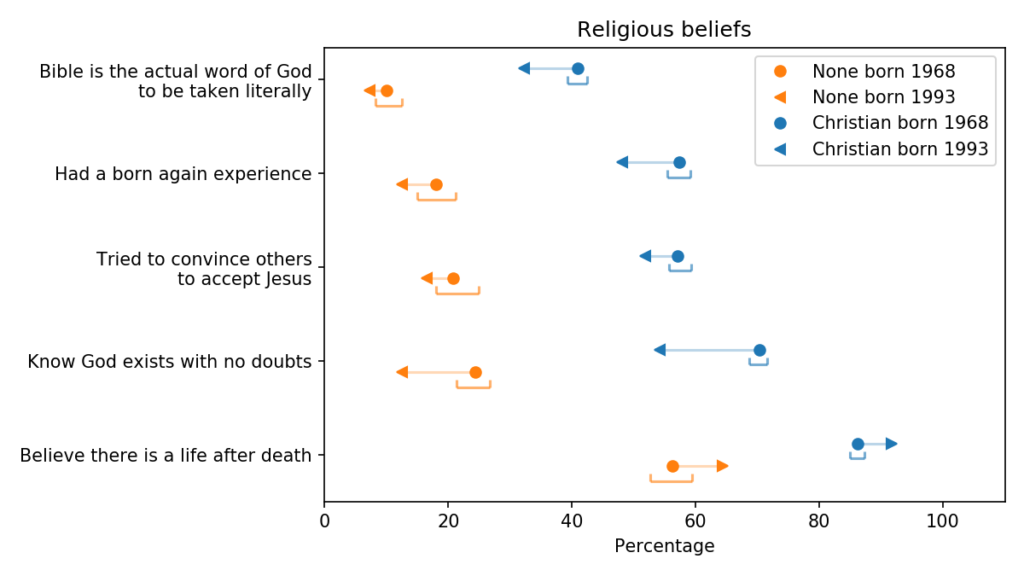
Generational changes in religious belief, comparing people born in 1968 and 1993

The blue markers are for Christians (people whose religious preference is Catholic, Protestant, or Christian); the orange markers are for people with no religious affiliation.

For each group, the circles show estimated percentages for people born in 1968; the arrowheads show percentages for people born in 1993.

For both groups, the estimates are for 2018, when the younger group was 25 and the older group was 50. The brackets show 90% confidence intervals for the estimates, computed by random resampling.

The top row shows the fraction of respondents who interpret the Christian bible literally; more specifically, when asked “Which of these statements comes closest to describing your feelings about the Bible?”, they chose the first of these options:

  • “The Bible is the actual word of God and is to be taken literally, word for word”
  • “The Bible is the inspired word of God but not everything in it should be taken literally, word for word.
  • “The Bible is an ancient book of fables, legends, history, and moral precepts recorded by men.”

Not surprisingly, people who consider themselves Christian are more likely to interpret the Bible literally, compared to people with no religious affiliation.

But younger Christians are less likely to be literalists than the previous generation. Most of the other variables show the same pattern; younger Christians are less likely to answer yes to these questions:

  • “Would you say you have been ‘born again’ or have had a ‘born again’ experience — that is, a turning point in your life when you committed yourself to Christ?”
  • “Have you ever tried to encourage someone to believe in Jesus Christ or to accept Jesus Christ as his or her savior?”

And they are less likely to report that they know God really exists; specifically, they were asked “Which statement comes closest to expressing what you believe about God?” and given these options:

  • I don’t believe in God
  • I don’t know whether there is a God and I don’t believe there is any way to find out.
  • I don’t believe in a personal God, but I do believe in a Higher Power of some kind.
  • I find myself believing in God some of the time, but not at others.
  • While I have doubts, I feel that I do believe in God.
  • I know God really exists and I have no doubts about it.

Younger Christians are less likely to say they know God exists and have no doubts.

Despite all that, younger Christians are more likely to believe in an afterlife. When asked “Do you believe there is a life after death?”, more than 90% say yes.

Among the unaffiliated, the trends are the same. Younger Nones are less likely to believe that the Bible is the literal word of God, less likely to have proselytized or been born again, and less likely to be sure God exists. But they are a little more likely to believe in an afterlife.

More questions, less religion

UPDATE: Since the first version of this article, I’ve had a chance to look at six other questions related to religious belief and activity. Here are the results:

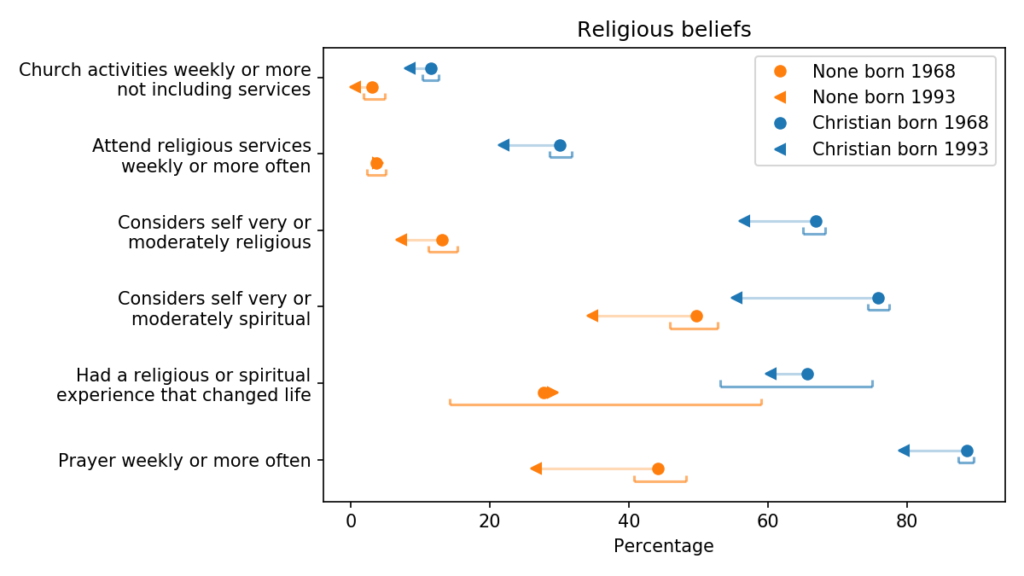
Generational changes in religious belief, comparing people born in 1968 and 1993

Qualitatively, these results are similar to what we saw before: controlling for period effects, younger Christians are more secular than the previous generation, in both beliefs and actions.

They are substantially less likely to consider themselves “religious” or “spiritual”, and less likely to attend religious services or pray weekly. And they are slightly less likely to participate in church activities other than services.

They might also be less likely to say they have had a life-changing religious experience, but that change falls within the margin of error.

In later articles, I’ll look at trends in other beliefs and attitudes, especially related to public policy. But first I should explain how I generated these estimates.

Methodology

My goal is to estimate generational changes, that is, cohort effects as distinguished from age and period effects. In general, it is not possible to distinguish between age, period, and cohort effects without making some assumptions. So this analysis is based on the assumption that age effects in this dataset are negligible compared to period and cohort effects.

Data from the General Social Survey goes back to 1972; it includes data from almost 65,000 respondents.

To measure current differences between people born in 1968 and 1993, I could select only respondents born in those years and interviewed in 2018. But there are not very many of them.

Alternatively, I could use data from all respondents, going back to 1972, fit a model, and use the model to estimate generational differences. That might work, but it would probably give too much weight to older, less relevant data.

As a compromise, I use data from 1998 to 2018, from respondents born in 1940 or later. This subset includes about 25,000 respondents. But not every respondent was asked every question, so the number of valid responses for most questions is smaller.

For most questions, I discard a small number of respondents who gave no response or said they did not know.

To model the responses, I use logistic regression with year of birth (cohort) and year of interview as independent variables. For questions with more than two responses, I choose one of the responses to study, usually the most popular; in a few cases, I grouped a subset of responses (for example “agree” and “strongly agree”).

I use a quadratic model for the period effect and a cubic model of the cohort effect, using visual tests to check whether the models do an acceptable job of describing the trends in the data.

I fit separate models for Christians and Nones, to allow for the possibility that trends might look different in the two groups (as it turns out they often do).

Then I use the models to generate predictions for four groups: Christians born in 1968 and 1993, and Nones born in the same years. These are “predictions” in the statistical sense of the word, but they are deliberately not extrapolations into cohorts or periods that are not in the dataset; it might be more correct to call them “interpolations”.

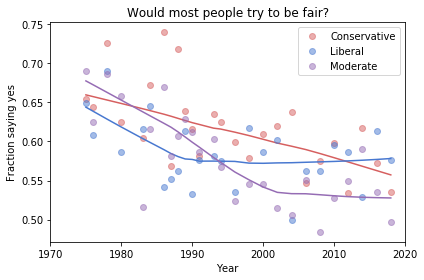
To show how this method works, let’s consider the fraction of Christians who answer that they know God exists, with no doubts. The following figure shows this fraction as a function of birth year (cohort):

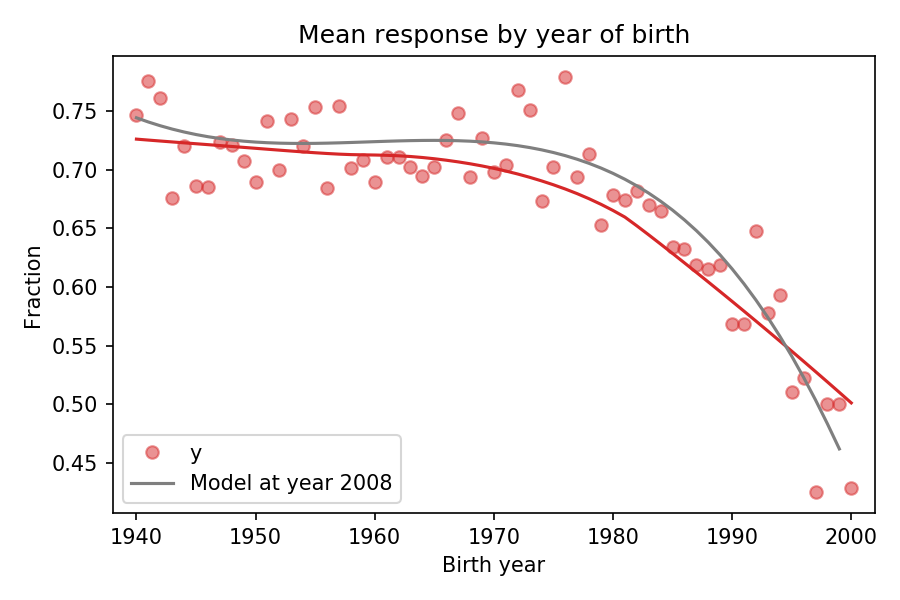
Fraction of Christians who says they know God exists, plotted over year of birth

The red dots show the fraction of respondents in each birth cohort. The red line shows a smooth curve through the data, computed by local regression (LOWESS). The gray line shows the predictions of the model for year 2008.

This figure shows that the logistic regression model of birth year does an acceptable job of describing the trends in the data, while also controlling for year of interview.

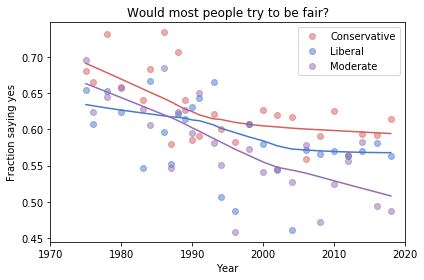
To see whether the model also describes trends over time, we can plot the fraction of respondents in each year of interview:

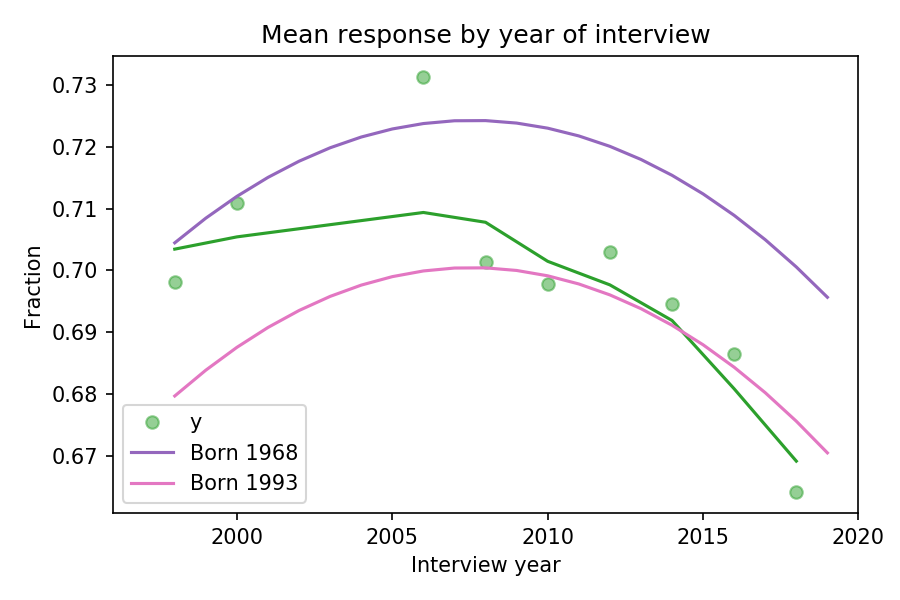
Fraction of Christians who says they know God exists, plotted over year of inteview

The green dots show the fraction of respondents during each year of interview and the green line shows a local regression through the data. The purple line shows the model’s predictions for someone born in 1968; the pink line shows predictions for someone born in 1993.

The gap between the purple and pink curves is the estimated generational change; in this example, it’s about 3 percentage points.

In summary, the model uses data from a range of birth years and interview years to fit a model, then uses the model to estimate the difference in response between people born in different years, both interviewed in 2018.

The results are based on the assumption that the model adequately describes the period and cohort effects, and that any age effects are negligible by comparison.

You can see all of the details in this Jupyter notebook, and you can click here to run it on Colab.

Please stop teaching people to write about science in the passive voice

Please stop teaching people to write about science in the passive voice

You might think you have to, but you don’t and you shouldn’t.

Why you might think you have to

  1. Science is objective and it doesn’t matter who does the experiment, so we should write in the passive voice, which emphasizes the methods and materials, not the scientists.
  2. You are teaching at <a level of education> and you have to prepare students for the <next level of education>, where they will be required to write in the passive voice.

Why you don’t have to

Regardless of how objective we think science is, writing about it in the passive voice doesn’t make it any more objective. Science is done by humans; there is no reason to pretend otherwise.

If you are teaching students to write in the passive voice because you think they need it at the next stage in the pipeline, you don’t have to.

If they learn to write in the active voice now, they can learn to write in the passive voice later, when and if they have to. And they might not have to.

A few years ago I surveyed the style guides of the top scientific journals in the world, and here’s what I found:

  1. None of them require the passive voice.
  2. Several of them have been begging scientists for decades to stop writing in the passive voice.

Here is the style guide from Science, from 1968, and it says:

“Choose the active voice more often than you choose the passive, for the passive voice usually requires more words and often obscures the agent of action.”

Here’s the style guide from Nature:

“Nature journals like authors to write in the active voice (“we performed the experiment…” ) as experience has shown that readers find concepts and results to be conveyed more clearly if written directly.”

From personal correspondence with the production department at the Proceedings of the National Academy of Sciences USA (PNAS), I learned:

“[We] feel that accepted best practice in writing and editing favors active voice over passive.”

Top journals agree: you don’t have to teach students to write in the passive voice.

Why you shouldn’t

As a stylistic matter, excessive use of the passive voice is boring. As a practical matter, it is unclear.

For example, the following is the abstract of a paper I read recently. It describes prior work that was done by other scientists and summarizes new work done by the author. See if you can tell which is which.

The Lotka–Volterra model of predator–prey dynamics was used for approximation of the well-known empirical time series on the lynx–hare system in Canada that was collected by the Hudson Bay Company in 1845–1935. The model was assumed to demonstrate satisfactory data approximation if the sets of deviations of the model and empirical data for both time series satisfied a number of statistical criteria (for the selected significance level). The frequency distributions of deviations between the theoretical (model) trajectories and empirical datasets were tested for symmetry (with respect to the Y-axis; the Kolmogorov–Smirnov and Lehmann–Rosenblatt tests) and the presence or absence of serial correlation (the Swed–Eisenhart and “jumps up–jumps down” tests). The numerical calculations show that the set of points of the space of model parameters, when the deviations satisfy the statistical criteria, is not empty and, consequently, the model is suitable for describing empirical data.

L. V. Nedorezov “The dynamics of the lynx–hare system: an application of the Lotka–Volterra model“.

Who used the model? Who assumed it was satisfactory? And who tested for symmetry?

I don’t know.

Please don’t teach students to write like this. It’s bad for them and anyone who has to read what they write, and it’s bad for science.

Handicapping pub trivia

Handicapping pub trivia

Introduction

The following question was posted recently on Reddit’s statistics forum:

If there is a quiz of x questions with varying results between teams of different sizes, how could you logically handicap the larger teams to bring some sort of equivalence in performance measure?

[Suppose there are] 25 questions and a team of two scores 11/25. A team of 4 scores 17/25. Who did better […]?

One respondent suggested a binomial model, in which every player has the same probability of answering any question correctly.

I suggested a model based on item response theory, in which each question has a level of difficulty, d, each player has a level of efficacy e, and the probability that a player answers a question is

expit(e-d+c)

where c is a constant offset for all players and questions and expit is the inverse of the logit function.

Another respondent pointed out that group dynamics will come into play. On a given team, it is not enough if one player knows the answer; they also have to persuade their teammates.

Me (left) at pub trivia with friends in Richmond, VA. Despite our numbers, we did not win.

I wrote some simulations to explore this question. You can see a static version of my notebook here, or you can run the code on Colab.

I implement a binomial model and a model based on item response theory. Interestingly, for the scenario in the question they yield opposite results: under the binomial model, we would judge that the team of two performed better; under the other model, the team of four was better.

In both cases I use a simple model of group dynamics: if anyone on the team gets a question, that means the whole team gets the question. So one way to think of this model is that “getting” a question means something like “knowing the answer and successfully convincing your team”.

Anyway, I’m not sure I really answered the question, other than to show that the answer depends on the model.

The Dartboard Paradox

The Dartboard Paradox

On November 5, 2019, I will be at PyData NYC to give a talk called The Inspection Paradox is Everywhere [UPDATE: The video from the talk is here]. Here’s the abstract:

The inspection paradox is a statistical illusion you’ve probably never heard of. It’s a common source of confusion, an occasional cause of error, and an opportunity for clever experimental design. And once you know about it, you see it everywhere.

The examples in the talk include social networks, transportation, education, incarceration, and more. And now I am happy to report that I’ve stumbled on yet another example, courtesy of John D. Cook.

In a blog post from 2011, John wrote about the following counter-intuitive truth:

For a multivariate normal distribution in high dimensions, nearly all the probability mass is concentrated in a thin shell some distance away from the origin.

John does a nice job of explaining this result, so you should read his article, too. But I’ll try to explain it another way, using a dartboard.

If you are not familiar with the layout of a “clock” dartboard, it looks like this:

File:Dartboard diagram.svg

I got the measurements of the board from the British Darts Organization rules, and drew the following figure with dimensions in mm:

Now, suppose I throw 100 darts at the board, aiming for the center each time, and plot the location of each dart. It might look like this:

Suppose we analyze the results and conclude that my errors in the x and y directions are independent and distributed normally with mean 0 and standard deviation 50 mm.

Assuming that model is correct, then, which do you think is more likely on my next throw, hitting the 25 ring (the innermost red circle), or the triple ring (the middlest red circle)?

It might be tempting to say that the 25 ring is more likely, because the probability density is highest at the center of the board and lower at the triple ring.

We can see that by generating a large sample, generating a 2-D kernel density estimate (KDE), and plotting the result as a contour.

In the contour plot, darker color indicates higher probability density. So it sure looks like the inner ring is more likely than the outer rings.

But that’s not right, because we have not taken into account the area of the rings. The total probability mass in each ring is the product of density and area (or more precisely, the density integrated over the area).

The 25 ring is more dense, but smaller; the triple ring is less dense, but bigger. So which one wins?

In this example, I cooked the numbers so the triple ring wins: the chance of hitting triple ring is about 6%; the chance of hitting the double ring is about 4%.

If I were a better dart player, my standard deviation would be smaller and the 25 ring would be more likely. And if I were even worse, the double ring (the outermost red ring) might be the most likely.

Inspection Paradox?

It might not be obvious that this is an example of the inspection paradox, but you can think of it that way. The defining characteristic of the inspection paradox is length-biased sampling, which means that each member of a population is sampled in proportion to its size, duration, or similar quantity.

In the dartboard example, as we move away from the center, the area of each ring increases in proportion to its radius (at least approximately). So the probability mass of a ring at radius r is proportional to the density at r, weighted by r.

We can see the effect of this weighting in the following figure:

The blue line shows estimated density as a function of r, based on a sample of throws. As expected, it is highest at the center, and drops away like one half of a bell curve.

The orange line shows the estimated density of the same sample weighted by r, which is proportional to the probability of hitting a ring at radius r.

It peaks at about 60 mm. And the total density in the triple ring, which is near 100 mm, is a little higher than in the 25 ring, near 10 mm.

If I get a chance, I will add the dartboard problem to my talk as yet another example of length-biased sampling, also known as the inspection paradox.

You can see my code for this example in this Jupyter notebook.

UPDATE November 6, 2019: This “thin shell” effect has practical consequences. This excerpt from The End of Average talks about designing the cockpit of a plan for the “average” pilot, and discovering that there are no pilots near the average in 10 dimensions.

What should you do?

What should you do?

In my previous post I asked “What should I do?“. Now I want to share a letter I wrote recently for students at Olin, which appeared in our school newspaper, Frankly Speaking.

It is addressed to engineering students, but it might also be relevant to people who are not students or not engineers.

Dear Students,

As engineers, you have a greater ability to affect the future of the planet than almost anyone else.  In particular, the decisions you make as you start your careers will have a disproportionate impact on what the world is like in 2100.

Here are the things you should work on for the next 80 years that I think will make the biggest difference:

  • Nuclear energy
  • Desalination
  • Transportation without fossil fuels
  • CO₂ sequestration
  • Alternatives to meat
  • Global education
  • Global child welfare
  • Infrastructure for migration
  • Geoengineering

Let me explain where that list comes from.

First and most importantly, we need carbon-free energy, a lot of it, and soon.  With abundant energy, almost every other problem is solvable, including food and desalinated water.  Without it, almost every other problem is impossible.

Solar, wind, and hydropower will help, but nuclear energy is the only technology that can scale up enough, soon enough, to substantially reduce carbon emissions while meeting growing global demand.

With large scale deployment of nuclear power, it is feasible for global electricity production to be carbon neutral by 2050 or sooner.  And most energy use, including heat, agriculture, industry, and transportation, could be electrified by that time. Long-range shipping and air transport will probably still require fossil fuels, which is why we also need to develop carbon capture and sequestration.

Global production of meat is a major consumer of energy, food, and water, and a major emitter of greenhouse gasses.  Developing alternatives to meat can have a huge impact on climate, especially if they are widely available before meat consumption increases in large developing countries.

World population is expected to peak in 2100 at 9 to 11 billion people.  If the peak is closer to 9 than 11, all of our problems will be 20% easier.  Fortunately, there are things we can do to help that happen, and even more fortunately, they are good things.

The difference between 9 and 11 depends mostly on what happens in Africa during the next 30 years.  Most of the rest of the world has already made the “demographic transition“, that is, the transition from high fertility (5 or more children per woman) to low fertility (at or below replacement rate).

The primary factor that drives the demographic transition is child welfare; increasing childhood survival leads to lower fertility.  So it happens that the best way to limit global population is to protect children from malnutrition, disease, and violence. Other factors that contribute to lower fertility are education and economic opportunity, especially for women.

Regardless of what we do in the next 50 years, we will have to deal with the effects of climate change, and a substantial part of that work will be good old fashioned civil engineering.  In particular, we need infrastructure like sea walls to protect people and property from natural disasters. And we need a new infrastructure of migration, including the ability to relocate large numbers of people in the short term, after an emergency, and in the long term, when current population centers are no longer viable.

Finally, and maybe most controversially, I think we will need geoengineering.  This is a terrible and dangerous idea for a lot of reasons, but I think it is unavoidable, not least because many countries will have the capability to act unilaterally.  It is wise to start experiments now to learn as much as we can, as long as possible before any single actor takes the initiative.

Think locally, act globally

When we think about climate change, we gravitate to individual behavior and political activism.  These activities are appealing because they provide opportunities for immediate action and a feeling of control.  But they are not the best tools you have.

Reducing your carbon footprint is a great idea, but if that’s all you do, it will have a negligible effect.

And political activism is great: you should vote, make sure your representatives know what you think, and take to the streets if you have to.  But these activities have diminishing returns. Writing 100 letters to your representative is not much better than one, and you can’t be on strike all the time.

If you focus on activism and your personal footprint, you are neglecting what I think is your greatest tool for impact: choosing how you spend 40 hours a week for the next 80 years of your life.

As an early-career engineer, you have more ability than almost anyone else to change the world.  If you use that power well, you will help us get through the 21st Century with a habitable planet and a high quality of life for the people on it.

What should I do?

What should I do?

I am planning to be on sabbatical from June 2020 to August 2021, so I am thinking about how to spend it. Let me tell you what I can do, and you can tell me what I should do.

Data Science

I consider myself a data scientist, but that means different things to different people. More specifically, I can contribute in the following areas:

  • Data exploration, modeling, and prediction,
  • Bayesian statistics and machine learning,
  • Scientific computing and optimization,
  • Software engineering and reproducible science,
  • Technical communication, including data visualization.

I have written a series of books related to data science and scientific computing, including Think Stats, Think Bayes, Physical Modeling in MATLAB, and Modeling and Simulation in Python.

And I practice what I teach. During a previous sabbatical, I was a Visiting Scientist at Google, working in their Make the Web Faster initiative. I worked on measurement and modeling of network performance, related to my previous research.

As a way of developing, demonstrating, and teaching data science skills, I write a blog called Probably Overthinking It.

Software Engineering

I’ve been programming since before you (the median-age reader of this article) were born, mostly in C for the first 20 years, and mostly in Python for the last 20. But I’ve also worked in Java, MATLAB, and a bunch of functional languages.

Most of my code has been for research or education, but in my time at Google I learned to write industrial-grade code with professional software engineering tools.

I work in public view, so you can see the good, the bad, and the ugly on GitHub. As a recent example, here’s a library I am designing for representing discrete probability distributions.

I work on teams: I have co-taught classes, co-authored books, consulted with companies and colleges, and collaborated on software projects. I’ve done Scrum training, and I use agile methods and tools on most of my projects (with varying degrees of fidelity).

Curriculum design

If you are creating a new college from scratch, I am one of a small number of people with that experience. When I joined Olin College in 2003, the first year curriculum had run once. I was in for the creation of Years 2, 3, and 4, as well as the reinvention of Year 1.

Since then, Olin has come to be recognized as a top undergraduate engineering program and a world leader in innovative education. I am proud of my work here and the amazing colleagues I have done it with.

My projects focus on the role of computing and data science in education, especially engineering education.

  1. I was part of a team that developed a novel introduction to computational modeling and simulation, and I wrote a book about it, now available for MATLAB and Python.
  2. I developed an introductory data science course for Olin, a book, and an online class. Currently I am working with a team at Harvard to develop a data science class for their GenEd program.
  3. Bayesian statistics is not just for grad students. I developed an undergraduate class that teaches Bayesian methods first, and wrote a book about it.
  4. Data structures is a problematic class in the Computer Science curriculum. I developed a class on Complexity Science as an alternative approach to the topic, and wrote a book about it. And for people coming to the topic later, I developed an online class and a book.

I have also written a series of books to help people learn to program in Python, Java, and C++. Other authors have adapted my books for Julia, Perl, OCaml, and other languages.

My books and curricular materials are used in universities, colleges, and high schools all over the world.

I have taught webcasts and workshops on these topics at conferences like PyCon and SciPy, and for companies developing in-house expertise.

If you are creating a new training program, department, or college, maybe I can help.

What I am looking for

I want to work on interesting projects with potential for impact. I am especially interested in projects related to the following areas, which are the keys we need to get through the 21st Century with a habitable planet and a high quality of life for the people on it:

  • Nuclear energy
  • Desalination
  • CO₂ sequestration
  • Geoengineering
  • Alternatives to meat
  • Transportation without fossil fuels
  • Global education
  • Global child welfare
  • Infrastructure for natural disaster and rising sea level

I live in Needham MA, and probably will not relocate for this sabbatical, but I could work almost anywhere in eastern Massachusetts. I would consider remote work, but I would rather work with people face to face, at least sometimes.

And I’ll need financial support for the year.

So, what should I do?

For more on my background, here is my CV.

What’s the frequency, Kenneth?

What’s the frequency, Kenneth?

First, if you get the reference in the title, you are old. Otherwise, let me google that for you.

Second, a Reddit user recently posted this question

I have temperatures reading over times (2 secs interval) in a computer that is control by an automatic fan. The temperature fluctuate between 55 to 65 in approximately sine wave fashion. I wish to find out the average time between each cycle of the wave (time between 55 to 65 then 55 again the average over the entire data sets which includes many of those cycles) . What sort of statistical analysis do I use?

[The following] is one of my data set represents one of the system configuration. Temperature reading are taken every 2 seconds. Please show me how you guys do it and which software. I would hope for something low tech like libreoffice or excel. Hopefully nothing too fancy is needed.

A few people recommended using FFT, and I agreed, but I also suggested two other options:

  1. Use a cepstrum, or
  2. Keep it simple and use zero-crossings instead.

And then another person suggested autocorrelation.

I ran some experiments to see what each of these solutions looks like and what works best. If you are too busy for the details, I think the best option is computing the distance between zero crossings using a spline fitted to the smoothed data.

If you want the details, they are in this Jupyter notebook.

Watch your tail!

Watch your tail!

For a long time I have recommended using CDFs to compare distributions. If you are comparing an empirical distribution to a model, the CDF gives you the best view of any differences between the data and the model.

Now I want to amend my advice. CDFs give you a good view of the distribution between the 5th and 95th percentiles, but they are not as good for the tails.

To compare both tails, as well as the “bulk” of the distribution, I recommend a triptych that looks like this:

There’s a lot of information in that figure. So let me explain.

The code for this article is in this Jupyter notebook.

Daily changes

Suppose you observe a random process, like daily changes in the S&P 500. And suppose you have collected historical data in the form of percent changes from one day to the next. The distribution of those changes might look like this:

If you fit a Gaussian model to this data, it looks like this:

It looks like there are small discrepancies between the model and the data, but if you follow my previous advice, you might look at these CDFs and conclude that the Gaussian model is pretty good.

If we zoom in on the middle of the distribution, we can see the discrepancies more clearly:

In this figure it is clearer that the Gaussian model does not fit the data particularly well. And, as we’ll see, the tails are even worse.

Survival on a log-log scale

In my opinion, the best way to compare tails is to plot the survival curve (which is the complementary CDF) on a log-log scale.

In this case, because the dataset includes positive and negative values, I shift them right to view the right tail, and left to view the left tail.

Here’s what the right tail looks like:

This view is like a microscope for looking at tail behavior; it compresses the bulk of the distribution and expands the tail. In this case we can see a small discrepancy between the data and the model around 1 percentage point. And we can see a substantial discrepancy above 3 percentage points.

The Gaussian distribution has “thin tails”; that is, the probabilities it assigns to extreme events drop off very quickly. In the dataset, extreme values are much more common than the model predicts.

The results for the left tail are similar:

Again, there is a small discrepancy near -1 percentage points, as we saw when we zoomed in on the CDF. And there is a substantial discrepancy in the leftmost tail.

Student’s t-distribution

Now let’s try the same exercise with Student’s t-distribution. There are two ways I suggest you think about this distribution:

1) Student’s t is similar to a Gaussian distribution in the middle, but it has heavier tails. The heaviness of the tails is controlled by a third parameter, ν.

2) Also, Student’s t is a mixture of Gaussian distributions with different variances. The tail parameter, ν, is related to the variance of the variances.

For a demonstration of the second interpretation, I recommend this animation by Rasmus Bååth.

I used PyMC to estimate the parameters of a Student’s t model and generate a posterior predictive distribution. You can see the details in this Jupyter notebook.

Here is the CDF of the Student t model compared to the data and the Gaussian model:

In the bulk of the distribution, Student’s t-distribution is clearly a better fit.

Now here’s the right tail, again comparing survival curves on a log-log scale:

Student’s t-distribution is a better fit than the Gaussian model, but it overestimates the probability of extreme values. The problem is that the left tail of the empirical distribution is heavier than the right. But the model is symmetric, so it can only match one tail or the other, not both.

Here is the left tail:

The model fits the left tail about as well as possible.

If you are primarily worried about predicting extreme losses, this model would be a good choice. But if you need to model both tails well, you could try one of the asymmetric generalizations of Student’s t.

The old six sigma

The tail behavior of the Gaussian distribution is the key to understanding “six sigma events”.

John Cook explains six sigmas in this excellent article:

“Six sigma means six standard deviations away from the mean of a probability distribution, sigma (σ) being the common notation for a standard deviation. Moreover, the underlying distribution is implicitly a normal (Gaussian) distribution; people don’t commonly talk about ‘six sigma’ in the context of other distributions.”

This is important. John also explains:

“A six-sigma event isn’t that rare unless your probability distribution is normal… The rarity of six-sigma events comes from the assumption of a normal distribution more than from the number of sigmas per se.”

So, if you see a six-sigma event, you should probably not think, “That was extremely rare, according to my Gaussian model.” Instead, you should think, “Maybe my Gaussian model is not a good choice”.

Left, right, part 4

Left, right, part 4

In the first article in this series, I looked at data from the General Social Survey (GSS) to see how political alignment in the U.S. has changed, on the axis from conservative to liberal, over the last 50 years.

In the second article, I suggested that self-reported political alignment could be misleading.

In the third article I looked at responses to this question:

Do you think most people would try to take advantage of you if they got a chance, or would they try to be fair?

And generated seven “headlines” to describe the results.

In this article, we’ll use resampling to see how much the results depend on random sampling. And we’ll see which headlines hold up and which might be overinterpretation of noise.

Overall trends

In the previous article we looked at this figure, which was generated by resampling the GSS data and computing a smooth curve through the annual averages.

This image has an empty alt attribute; its file name is image.png

If we run the resampling process two more times, we get somewhat different results:

Now, let’s review the headlines from the previous article. Looking at different versions of the figure, which conclusions do you think are reliable?

  • Absolute value: “Most respondents think people try to be fair.”
  • Rate of change: “Belief in fairness is falling.”
  • Change in rate: “Belief in fairness is falling, but might be leveling off.”

In my opinion, the three figures are qualitatively similar. The shapes of the curves are somewhat different, but the headlines we wrote could apply to any of them.

Even the tentative conclusion, “might be leveling off”, holds up to varying degrees in all three.

Grouped by political alignment

When we group by political alignment, we have fewer samples in each group, so the results are noisier and our headlines are more tentative.

Here’s the figure from the previous article:

This image has an empty alt attribute; its file name is image-1.png

And here are two more figures generated by random resampling:

Now we see more qualitative differences between the figures. Let’s review the headlines again:

  • Absolute value: “Moderates have the bleakest outlook; Conservatives and Liberals are more optimistic.” This seems to be true in all three figures, although the size of the gap varies substantially.
  • Rate of change: “Belief in fairness is declining in all groups, but Conservatives are declining fastest.” This headline is more questionable. In one version of the figure, belief is increasing among Liberals. And it’s not at all clear the the decline is fastest among Conservatives.
  • Change in rate: “The Liberal outlook was declining, but it leveled off in 1990.” The Liberal outlook might have leveled off, or even turned around, but we could not say with any confidence that 1990 was a turning point.
  • Change in rate: “Liberals, who had the bleakest outlook in the 1980s, are now the most optimistic”. It’s not clear whether Liberals have the most optimistic outlook in the most recent data.

As we should expect, conclusions based on smaller sample sizes are less reliable.

Also, conclusions about absolute values are more reliable than conclusions about rates, which are more reliable than conclusions about changes in rates.