I’m happy to report that copyediting of Modeling and Simulation in Python is done, and the book is off to the printer! Electronic versions are available now from No Starch Press; print copies will be available in May, but you can pre-order now from No Starch Press, Amazon, and Barnes and Noble.

To celebrate, I just published one of the case studies from the end of Part I, which is about simulating discrete systems. The case study explores a classic question from queueing theory:

Suppose you are designing the checkout area for a new store. There is room for two checkout counters and a waiting area for customers. You can make two lines, one for each counter, or one line that serves both counters.

In theory, you might expect a single line to be better, but it has some practical drawbacks: in order to maintain a single line, you would have to install rope barriers, and customers might be put off by what seems to be a longer line, even if it moves faster.

So you’d like to check whether the single line is really better and by how much.

Simulation can help answer this question. The following figure shows the three scenarios I simulated:

The leftmost diagram shows a single queue (with customers arriving at rate 𝜆) and a single server (with customers completing service at rate 𝜇).

The center diagram shows a single queue with two servers, and the rightmost diagram shows two queue with two servers.

So, which is the best, and by how much? You can read my answer in the online version of the book. Or you can run the Jupyter notebook on Colab.

Here’s what some of the results look like:

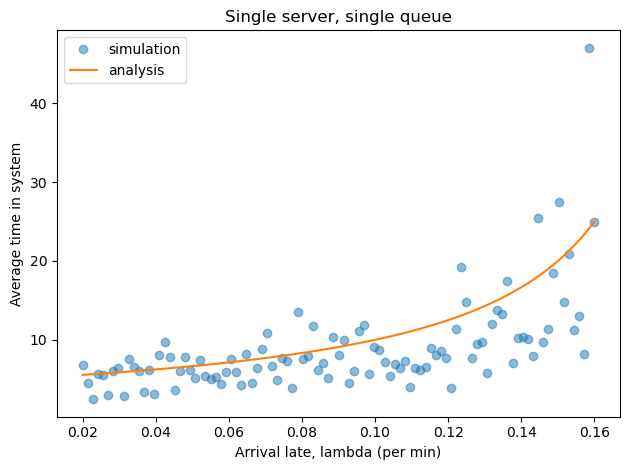
This figure shows the time customers are in the system, including wait time and service time, as a function of the arrival rate. The orange line shows the average we expect based on analysis; the blue dots show the result of simulations.

This comparison shows that the simulation and analysis are consistent. It also demonstrates one of the features of simulation: it is easy to quantify not just the average we expect but also the variation around the average.

That capability turns out to be useful for this problem because, as it turns out, the difference between the one-queue and two-queue scenarios is small compared to the variation, which suggests the advantage would be unnoticed in practice.

I conclude:

The two configurations are equally good as long as both servers are busy; the only time two lines is worse is if one queue is empty and the other contains more than one customer. In real life, if we allow customers to change lanes, that disadvantage can be eliminated.

From a theoretical point of view, one line is better. From a practical point of view, the difference is small and can be mitigated. So the best choice depends on practical considerations.

On the other hand, you can do substantially better with an express line for customers with short service times. But that’s a topic for another case study.